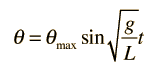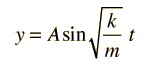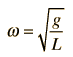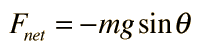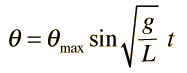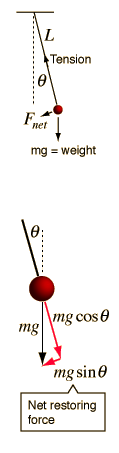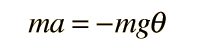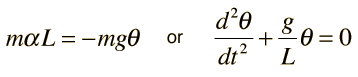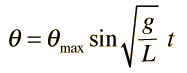M.A.S- pendulo simple
- PENDULO SIMPLE
Un péndulo simple es uno tal, que se puede considerar como una masa puntual, suspendida de una cuerda o varilla de masa despreciable. Es un sistema resonante con una frecuencia de resonancia simple. Para pequeñas amplitudes, el periodo de tal péndulo, se puede aproximar por:
MOVIMIENTO DEL PENDULO
El movimiento de un péndulo simple es como un movimiento armónico simple en donde la ecuación para el desplazamiento angular es
Que tiene la misma forma que el movimiento de una masa sobre un muelle:
La frecuencia angular del movimiento está dada por
comparada a para una masa sobre un muelle.
La frecuencia del péndulo en Hz está dada por
y el periodo del movimiento es entonces
LEYES DEL PENDULO
- El periodo de osilacion de un pendulo es independiente de la masa
- el periodo de un pendulo es directamente proporcional a la raiz cuadrada de la longitud
- el periodo de un pendulo es inversamente proporcional a la raiz cuadrada de la gravedad
- para pequeños angulos los periodos seran iguales (angulos menores de 10)
PERIODO DEL PENDULO SIMPLE
Una masa puntual colgando de una cuerda sin masa, es un ejemplo idealizado de un péndulo simple. Cuando se desplaza desde su punto de equilibrio, la fuerza de restauración que lo trae de nuevo al centro, está dada por:
Para pequeños ángulos θ, podemos usar la aproximación
en cuyo caso la segunda ley de Newton toma la forma
Aún en este caso aproximado, la solución de la ecuación hace uso de las ecuaciones y cálculo diferencial. La ecuación diferencial es
y para pequeños ángulos θ la solución es:
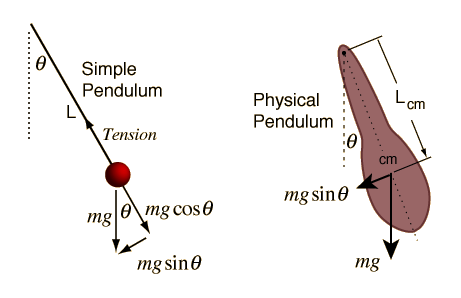
GEOMETRIA DEL PENDULO
ECUACIONES DE UN PENDULO
La ecuación de movimiento para el péndulo simple para amplitudes suficientemente pequeñas tiene la forma
La cual, cuando se pone en forma angular viene a ser
Esta ecuación diferencial es como la del oscilador armónico simple y tiene la solución: